Implementing Proximal Policy Optimization in JAX

In this article we will go in depth into implementing PPO using JAX. You can find the code repository here.

Introduction

Proximal Policy Optimization (PPO) is a policy gradient algorithm that incorporates concepts from trust regions, function approximation, and model-free reinforcement learning. In practice, PPO commonly uses artificial neural networks as function approximators, making it a key method in deep reinforcement learning. PPO has achieved notable success across various Gymnasium tasks and has even been used for post-deployment training of models like ChatGPT. The core idea of PPO is a clipped objective function, which helps maintain a trust region during optimization and stabilizes training.

Characteristic	Description
Algorithm Type	Policy Gradient
Trust Region	Clipped surrogate objective
Function Approximator	Neural Networks (typically MLPs or CNNs)
On/Off Policy	On-policy
Online/Offline	Online

Before we dive into implementing PPO let’s cover some background topics to get a better understanding.

Background

Policy Gradient Methods

In policy gradients we are conerned with maximizing an often parameterized scalar performance measure \(\mathcal{J}(\mathbf{\theta})\). To place the gradient into policy-gradient we use the following estimator for the performance gradient:

\[ \nabla{\mathcal{J}(\mathbf{\theta_t})} \propto \mathbb{E}_t \left[ \nabla_\theta \log \pi_\theta(a_t|s_t) \, \hat{G}_t \right] \]

Where \(\hat{G}_t\) can be (but doesn’t have to) the general advantage estimation: \[ \hat{G}_t = \sum_{i=0}^{T-t-1} (\gamma \lambda)^i \, \delta_{t+i} \]

where \(\delta_t\) is the TD error: \[ \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) \]

Trust Region Policy Optimization

We can express TRPO as a constrained optimization problem:

\[\begin{align} \max_{\theta} \quad & \mathbb{E}_{t} \left[ \frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} \hat{G}_t \right] \\ \text{subject to} \quad & \mathbb{E}_{t} \left[ \mathrm{KL}\left( \pi_{\theta_{\text{old}}}(\cdot|s) \,\|\, \pi_\theta(\cdot|s) \right) \right] \leq \epsilon \end{align}\]

This is essentially saying, “Optimize performance, but do it cautiously.” In other words, the constraint prevents the policy from diverging too much from the old policy and limits changes to a so called trust region specified by the parameter \(\epsilon\).

PPO

The main performance objective from PPO clips the objective \(\frac{\pi_\theta(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} \hat{G}_t\) within the Trust Region boundaries represented by the interval \([1-\epsilon, 1+\epsilon]\):

\[ \mathcal{J}^{CLIP}(\theta) = \mathbb{E}_t \left[ \min \left( \rho_t(\theta) \hat{G}_t, \, \mathrm{clip}(\rho_t(\theta), 1-\epsilon, 1+\epsilon) \hat{G}_t \right) \right] \]

Where \(\rho_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)}\)

To visualize the effect of this clipping let’s consider a toy problem with a single parameter \(\theta \in \mathbb{R}\) which creates the parameterized policy

\[ \pi_\theta(a) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left( -\frac{(a - \theta)^2}{2\sigma^2} \right) \]

where \(\sigma\) is the standard deviation of the normal distribution.

import jax
import numpy as np
from jax import numpy as jnp
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['text.usetex'] = True
plt.rcParams.update({
    "font.size": 22,              # Global font size
    "axes.titlesize": 20,         # Axes title
    "axes.labelsize": 22,         # X/Y axis labels
    "xtick.labelsize": 18,
    "ytick.labelsize": 18,
    "legend.fontsize": 20,
    "figure.titlesize": 30        # suptitle
})

theta_old = 0.5
theta = 0.51
sigma = 0.1
a = jnp.linspace(0, 1, 200)

pi_theta_old = lambda action: (1 / (jnp.sqrt(2 * jnp.pi) * sigma)) * jnp.exp(-0.5 * ((action - theta_old) / sigma) ** 2)
pi_theta = lambda action: (1 / (jnp.sqrt(2 * jnp.pi) * sigma)) * jnp.exp(-0.5 * ((action - theta) / sigma) ** 2)

plt.figure(figsize=(8, 6))
plt.plot(a, jax.vmap(pi_theta_old)(a), label=r'$\pi_{\theta_{old}}(a)$')
plt.plot(a, jax.vmap(pi_theta)(a), label=r'$\pi_{\theta}(a)$')
plt.xlabel('Action $a$')
plt.ylabel('Probability Density')
plt.title(r'Policy Distributions for Different $\theta$')
plt.legend()
plt.grid(True)
plt.show()

Considering these two distributions let’s visualize \(\rho(\theta)\):

rho_theta = lambda action: pi_theta(action)/ pi_theta_old(action)
plt.figure(figsize=(8,6))
plt.plot(a, jax.vmap(rho_theta)(a), label=r'$\rho(\theta)$')
plt.xlabel(r'Action $a$')
plt.ylabel(r'$\rho(\theta)$')
plt.title(r'Sampling Ratio')
plt.legend()
plt.grid(True)
plt.show()

Now imagine at a given time step we receive \(\hat{G}_t = 1\) as our advantage estimate, the loss function (unclipped objective) will have the following form

L_unclipped = lambda action, G: G * rho_theta(action)
fig, axes = plt.subplots(1, 2, figsize=(16,6))
axes[0].plot(jax.vmap(rho_theta)(a), jax.vmap(L_unclipped, in_axes=(0, None))(a, 1.0), label=r'$L(\theta)$')
axes[0].set_xlabel(r'$\rho(\theta)$')
axes[0].set_ylabel(r'$J(\theta)$')
axes[0].set_title(r'$J(\theta)$, $G > 0$')
axes[0].grid(True)

axes[1].plot(jax.vmap(rho_theta)(a), jax.vmap(L_unclipped, in_axes=(0, None))(a, -1.0), label=r'$L(\theta)$')
axes[1].set_xlabel(r'$\rho(\theta)$')
axes[1].set_ylabel(r'$J(\theta)$')
axes[1].set_title(r'$J(\theta)$, $G < 0$')
axes[1].grid(True)
plt.suptitle("Unclipped Objective")
plt.show()

Now let’s apply the clipping the get our clipped surrogate objective used in PPO (\(\epsilon=0.2\)):

clip = 0.2
L_clipped = lambda action, G: G * jnp.minimum(rho_theta(action), jnp.clip(rho_theta(action), 1-clip, 1+clip))

fig, axes = plt.subplots(2, 2, figsize=(24, 24))
for ax_row in axes:
    for ax in ax_row:
        ax.tick_params(axis='both', which='major', labelsize=22)
        ax.title.set_size(28)
        ax.xaxis.label.set_size(26)
        ax.yaxis.label.set_size(26)

axes[0][0].plot(jax.vmap(rho_theta)(a), 
    jax.vmap(L_clipped, in_axes=(0, None))(a, 1.0), 
    label=r'$J^{CLIP}(\theta), G > 0$')
axes[0][0].set_title(r'$J^{CLIP}(\theta), G > 0$')
axes[0][0].set_xlabel(r'$\rho(\theta)$')
axes[0][0].set_ylabel(r'$J^{CLIP}(\theta)$') 
axes[0][0].grid(True)

axes[0][1].plot(jax.vmap(rho_theta)(a), 
    jax.vmap(L_clipped, in_axes=(0, None))(a, -1.0), 
    label=r'$J^{CLIP}(\theta), G < 0$')
axes[0][1].set_title(r'$J^{CLIP}(\theta), G > 0$')
axes[0][1].set_xlabel(r'$\rho(\theta)$')
axes[0][1].set_ylabel(r'$J^{CLIP}(\theta)$')
axes[0][1].grid(True)

grad_clipped_loss = jax.grad(L_clipped)

axes[1][0].plot(jax.vmap(rho_theta)(a), 
    jax.vmap(grad_clipped_loss, in_axes=(0, None))(a, 1.0), 
    label=r'$\nabla J^{CLIP}(\theta), G > 0$')
axes[1][0].set_title(r'$\nabla J^{CLIP}(\theta), G > 0$')
axes[1][0].set_xlabel(r'$\rho(\theta)$')
axes[1][0].set_ylabel(r'$\nabla J^{CLIP}(\theta)$')
axes[1][0].grid(True)

axes[1][1].plot(jax.vmap(rho_theta)(a), 
    jax.vmap(grad_clipped_loss, in_axes=(0, None))(a, -1.0), 
    label=r'$\nabla J^{CLIP}(\theta), G < 0$')
axes[1][1].set_title(r'$\nabla J^{CLIP}(\theta), G < 0$')
axes[1][1].set_xlabel(r'$\rho(\theta)$')
axes[1][1].set_ylabel(r'$\nabla J^{CLIP}(\theta)$')
axes[1][1].grid(True)
plt.suptitle("Clipped Objective")
plt.show()

Implementation Details in Discrete Action Space

The implementation details listed here are based on commit id 708816a. So make sure to check this out using git if you’re trying to follow along and the code and article are out of sync. I’m going to continue to improve and develop PPO-JAX in the future.

Psuedocode

\begin{algorithm} \caption{Proximal Policy Optimization} \begin{algorithmic} \State Initialize Actor and Critic Networks \State Initialize Actor Optimizer with $\alpha_{actor}$ \State Initialize Critic Optimizer with $\alpha_{critic}$ \State T $\leftarrow$ Total time-steps \State N $\leftarrow$ Number of parallel envs \State M $\leftarrow$ Number of minibatches \State S $\leftarrow$ Number of rollout steps \State Epochs $\leftarrow$ Number of training epochs \State Batch Size $\leftarrow$ N $\times$ S \State Minibatch Size $\leftarrow$ $\frac{Batch\,Size}{M}$ \State Iterations $\leftarrow$ $\frac{T}{Batch\,Size}$ // How many batches can you collect over T time steps? \State Initialize Rollout Buffer \For{i in Iterations} \For{t in S} \State Rollout Buffer $\leftarrow$ Collect Rollout Statistics \EndFor \For{t in reverse S} \State Compute $G_t$ using Rollout Buffer // General Advantage Estimate \EndFor \For{epoch in Epochs} \For{minibatch in Range(0, Batch Size, Minibatch Size)} \State Sample Random MiniBatch from Batch \State $\mathcal{L}_{Critic}(\mathbf{\psi})$ $\leftarrow$ $\frac{1}{\text{Minibatch Size}} \sum_{(s, G) \in \text{MiniBatch}} (V(s, \mathbf{\psi}) - G)^2$ \State $\mathcal{J}_{Actor}(\mathbf{\theta})$ $\leftarrow$ $\frac{1}{\text{Minibatch Size}} \sum_{(s, a, G) \in \text{MiniBatch}} \min \left( \rho(\mathbf{\theta}) G, \mathrm{clip}(\rho(\mathbf{\theta}), 1-\epsilon, 1+\epsilon) G \right) + c_{entropy} * \mathcal{H}(\pi_\theta(\cdot|s))$ \State $\mathbf{\psi} \gets \mathbf{\psi} - \alpha_{critic} \nabla_{\mathbf{\psi}} \mathcal{L}_{Critic}(\mathbf{\psi})$ \State $\mathbf{\theta} \gets \mathbf{\theta} + \alpha_{actor} \nabla_{\mathbf{\theta}} \mathcal{J}_{Actor}(\mathbf{\theta})$ \EndFor \EndFor \EndFor \end{algorithmic} \end{algorithm}

Rollout Buffer

This is where we collect the episode values and statistics.

obs = np.zeros((args.num_steps, args.num_envs) +\
        envs.single_observation_space.shape) # (S, N, D): D is the observation vector size
actions = np.zeros((args.num_steps, args.num_envs) +\
        envs.single_action_space.shape) # (S, N, A): A is the number of Action
logprobs = np.zeros((args.num_steps, args.num_envs)) # (S, N)
rewards = np.zeros((args.num_steps, args.num_envs)) # (S, N)
dones = np.zeros((args.num_steps, args.num_envs)) # (S, N)
values = np.zeros((args.num_steps, args.num_envs)) # (S, N)

At first it may seem more intuitive to have the number of environments as the first dimension. But this makes the application of value functions and other rollout statistics across dimensions of the parallel environments given a certain time step easier. In other words, it’s easier to do obs[step] = next_obs than obs[:, step] = next_obs. To drive this point home consider this example:

import numpy as np
from pprint import pprint
np.random.seed(0)
num_steps = 2
num_envs = 4
D = 3 # observation length

obs_buffer = np.zeros((num_steps, num_envs, D))
obs_buffer_alt = np.zeros((num_envs, num_steps, D)) 

print("Before")
print("obs_buffer shape:", obs_buffer.shape)
print("obs_buffer contents:")
pprint(obs_buffer)
print("obs_buffer_alt shape:", obs_buffer_alt.shape)
print("obs_buffer_alt contents:")
pprint(obs_buffer_alt)
step = 0

next_obs = np.random.randn(num_envs, D)
obs_buffer[step] = next_obs
obs_buffer_alt[:, step] = next_obs
print("After")
print("obs_buffer shape:", obs_buffer.shape)
print("obs_buffer contents:")
pprint(obs_buffer)
print("obs_buffer_alt shape:", obs_buffer_alt.shape)
print("obs_buffer_alt contents:")
pprint(obs_buffer_alt)

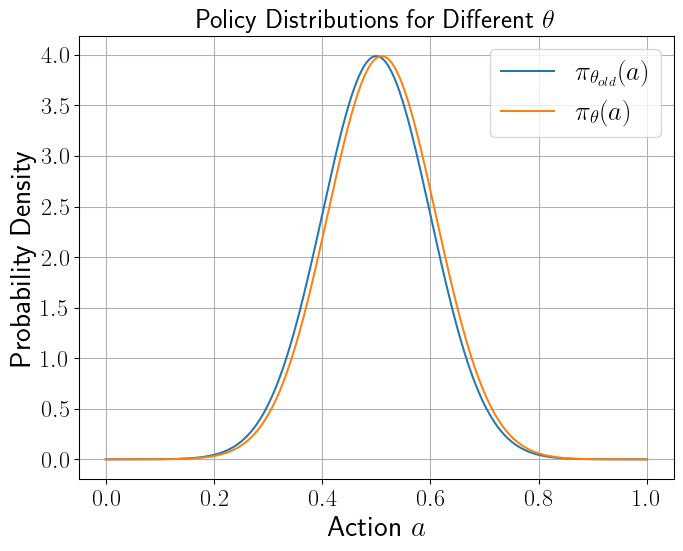
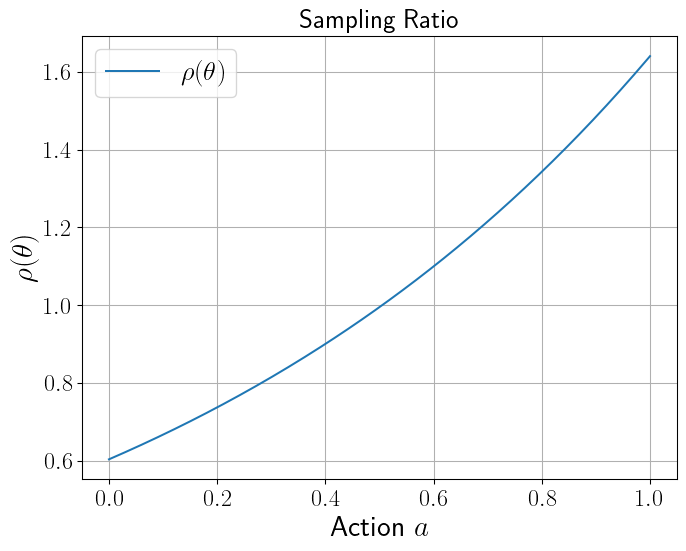
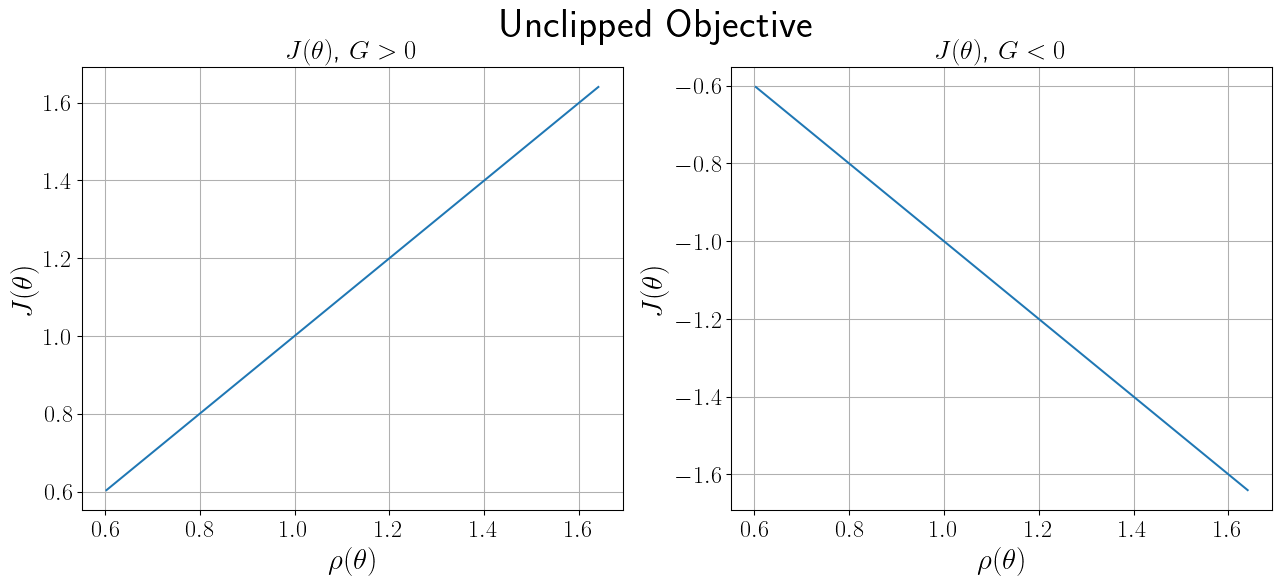
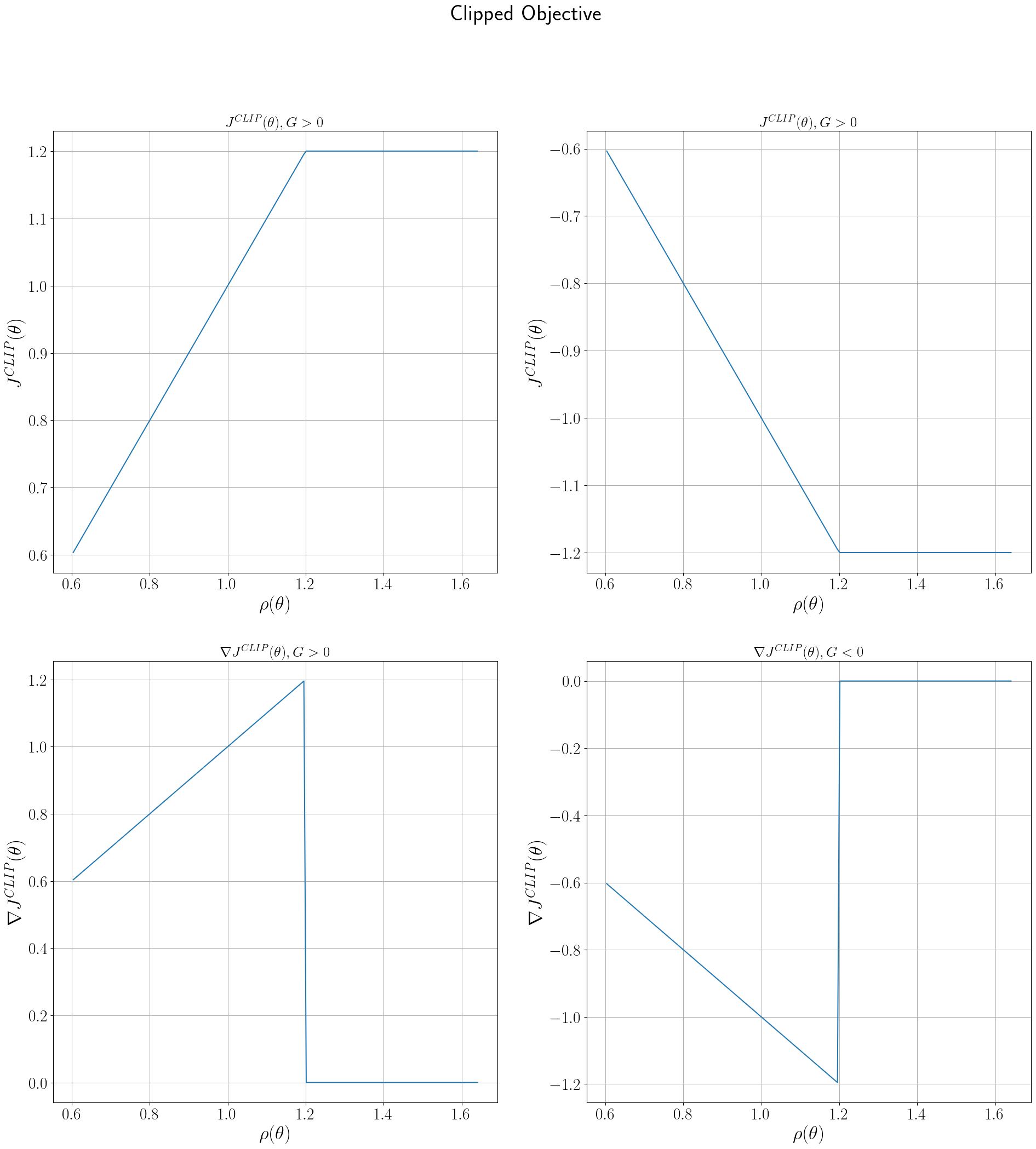
Before
obs_buffer shape: (2, 4, 3)
obs_buffer contents:
array([[[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.],
        [0., 0., 0.]]])
obs_buffer_alt shape: (4, 2, 3)
obs_buffer_alt contents:
array([[[0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.]],

       [[0., 0., 0.],
        [0., 0., 0.]]])
After
obs_buffer shape: (2, 4, 3)
obs_buffer contents:
array([[[ 1.76405235,  0.40015721,  0.97873798],
        [ 2.2408932 ,  1.86755799, -0.97727788],
        [ 0.95008842, -0.15135721, -0.10321885],
        [ 0.4105985 ,  0.14404357,  1.45427351]],

       [[ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ],
        [ 0.        ,  0.        ,  0.        ]]])
obs_buffer_alt shape: (4, 2, 3)
obs_buffer_alt contents:
array([[[ 1.76405235,  0.40015721,  0.97873798],
        [ 0.        ,  0.        ,  0.        ]],

       [[ 2.2408932 ,  1.86755799, -0.97727788],
        [ 0.        ,  0.        ,  0.        ]],

       [[ 0.95008842, -0.15135721, -0.10321885],
        [ 0.        ,  0.        ,  0.        ]],

       [[ 0.4105985 ,  0.14404357,  1.45427351],
        [ 0.        ,  0.        ,  0.        ]]])

A couple of things stand out:

• The assignment operator in the first buffer is easier.
• The values are grouped closer together, which potentially improves information retrieval.

Training Loop

    for iteration in range(1, args.num_iterations + 1): # number of iterations is calculated during run-time (check psuedo-code)
        
        for step in range(0, args.num_steps): # Rollout steps specified by the user and passed using `tyro` args
            # Collect Rollout
        
        for t in reversed(range(args.num_steps)): # Going through the steps backwards and dynamically calculating advantage functions
            # Compute GAE (General Advantage Esimtation)

        # prepare rollout batches
        
        for epoch in range(args.update_epochs): # train for this number of epochs specified 
            # ...
            
            for start in range(0, args.batch_size, args.minibatch_size): # sample minibatches and optimizes losses over minibatches
                # Optimize over minibatches

Actor and Critic Networks

To have a value function we need to create a critic neural network. A simple multi-layered perceptron works well for our purposes:

class Critic(nn.Module):
    @nn.compact
    def __call__(self, x):
        x = nn.Dense(64, kernel_init=layer_init(np.sqrt(2)))(x)
        x = nn.tanh(x)
        x = nn.Dense(64, kernel_init=layer_init(np.sqrt(2)))(x)
        x = nn.tanh(x)
        x = nn.Dense(1, kernel_init=layer_init(1.0))(x)
        return x.squeeze(-1)

class Actor(nn.Module):
    action_dim: int
    
    @nn.compact
    def __call__(self, x):
        x = nn.Dense(64, kernel_init=layer_init(np.sqrt(2)))(x)
        x = nn.tanh(x)
        x = nn.Dense(64, kernel_init=layer_init(np.sqrt(2)))(x)
        x = nn.tanh(x)
        x = nn.Dense(self.action_dim, kernel_init=layer_init(0.01))(x)
        return x

To initialize the model we may do something params = model.init(rng, jnp.ones(obs_shape)) where obs_shape is the dimensions of a single observation sample. You maybe wondering but we are dealing with batches of data and a rollout of steps S. How do we do a forwar pass or (apply in JAX lingo) over a larger dimension. This is where JAX conveniently shines through and gives us vmap:

def value_fn(params, obs): 
    value = jax.vmap(lambda x: critic_state.apply_fn(params, x))(obs) # dyncamically scales function to batch dimensions 
    return value


def policy_fn(params, obs):
    return jax.vmap(lambda x: actor_state.apply_fn(params, x))(obs)

Performing Rollout

During rollout we compute statistics state/observation values and sample actions during the policy:

Show Corrosponding Math

\[ \hat{V}(S, \mathbf{\psi}) \]

value = value_fn(critic_state.params, next_obs)

Now sampling an action from a discrete action-space created using logits from the actor network takes more work:

Show Corrosponding Math

\[ a \sim \pi(\cdot|s, \mathbf{\theta}) \]

logits = policy_fn(actor_state.params, next_obs)
rng, action_key = jax.random.split(rng)
action = jax.random.categorical(action_key, logits)

The nuances from using jax.random.split and jax.random.categorical really reflect the gap between going from math symbols and theory to a working code. Make sure to checkout how a rollout is collected in the code.

Computing Advantages \(\hat{G}_t\)

Show Corrosponding Math

\[ \hat{G}_t = \sum_{i=0}^{T-t-1} (\gamma \lambda)^i \, \delta_{t+i} \]

\[ \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) \]

for t in reversed(range(args.num_steps)):
    if t == args.num_steps - 1:
        mask = 1.0 - next_done
        next_values = next_value
    else:
        mask = 1 - dones[t+1]
        next_values = values[t+1]
    
    td_error =\
        rewards[t] +\
            args.gamma * next_values * mask -\
            values[t]
    last_gae_lambda = td_error +\
        args.gamma * args.gae_lambda * mask * last_gae_lambda        
    advantages[t] = last_gae_lambda
returns = advantages + values

Loss Function and Objective

We want to minimize the state value errors and maximize the policy objective. In the code I call both of these measures “loss”. One is the actor_loss_fn and the other critic_loss_fn. It would be more appropriate to rename actor_loss_fn. Something for future iterations.

Show Corrosponding Math

\[ \mathcal{J}^{CLIP}(\theta) = \min \left( \rho(\theta) \hat{G}, \, \mathrm{clip}(\rho(\theta), 1-\epsilon, 1+\epsilon) \hat{G} \right) \]

\[ \mathcal{J}_{Actor}(\theta) = \frac{1}{|\text{Minibatch}|} \sum_{(s, a, \hat{G}) \in \text{Minibatch}} L^{CLIP}(\theta) + c_{entropy} \cdot \mathcal{H}(\pi_\theta(\cdot|s)) \]

def actor_loss_fn(params, obs_batch, action, old_logprobs, advantages):
    logits = policy_fn(params, obs_batch)
    log_probs = jax.nn.log_softmax(logits)
    probs = jax.nn.softmax(logits)
    action = action.astype(jnp.int32)
    new_selected_log_prob = jnp.take_along_axis(log_probs, action[:, None], axis=1).squeeze(-1)
    entropy = -jnp.sum(probs * log_probs, axis=-1)
    log_ratio = new_selected_log_prob - old_logprobs
    ratio = jnp.exp(log_ratio)
    if args.norm_adv:
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
    pg_loss1 = advantages * ratio
    pg_loss2 = advantages * jnp.clip(ratio, 1 - args.clip_coef, 1 + args.clip_coef)
    pg_loss = jnp.minimum(pg_loss1, pg_loss2).mean()
    entropy_loss = entropy.mean()
    approx_kl = ((ratio - 1.0) - log_ratio).mean()
    return -(pg_loss + args.ent_coef * entropy_loss), approx_kl  # negative for gradient ascent

Show Corrosponding Math

\[ \mathcal{L}_{\text{Critic}}(\mathbf{\psi}) = \frac{1}{|\text{Minibatch}|} \sum_{(s, G) \in \text{Minibatch}} \left( V(s, \mathbf{\psi}) - G \right)^2 \]

def critic_loss_fn(params, obs_batch, returns):
    value = value_fn(params, obs_batch)
    
    v_loss = ((value - returns) ** 2)
    if args.clip_vloss:
        v_loss_clipped = jnp.clip(v_loss, -args.clip_coef, args.clip_coef)
        v_loss = jnp.maximum(v_loss, v_loss_clipped)
                    
    return 0.5 * v_loss.mean()

Update Step

Now that we can compute loss and objective we can use this to optimize our networks.

Show Corrosponding Math

\[ \mathbf{\psi} \gets \mathbf{\psi} - \alpha_{critic} \nabla_{\mathbf{\psi}} \mathcal{L}_{\text{Critic}}(\mathbf{\psi}) \]

\[ \mathbf{\theta} \gets \mathbf{\theta} + \alpha_{actor} \nabla_{\mathbf{\theta}} \mathcal{J}_{\text{Actor}}(\mathbf{\theta}) \]

(actor_loss, approx_kl), actor_grad =\
    value_and_grad(actor_loss_fn, has_aux=True)(actor_state.params, mb_obs, mb_actions, mb_logprobs, mb_advantages)
critic_loss, critic_grad = \
    value_and_grad(critic_loss_fn)(critic_state.params, mb_obs, mb_returns)
# Update states
critic_state = critic_state.apply_gradients(grads=critic_grad)
actor_state = actor_state.apply_gradients(grads=actor_grad)

Final Thoughts

Combining the rollout, loss computation, and optimization steps, we get our very own Proximal Policy Optimization algorithm in JAX (Yay! 🎉🤖), ready to be used on some cool control tasks (Checkout Results section next). Here are some final thoughts:

• JIT could speed things up a lot when done right but can also slow things down and make it worse. A good rule of thumb is to JIT functions where the parameter sizes are fixes and won’t change during runtime. This ensures that we don’t incur overhead from recompiling the same function over and over.
• Optax has a useful feature for reducing learning rate as the episode progresses. Use this to “anneal” your learning rate.
• This implementation of PPO fails in the MointainCar task. What could be wrong? Food for thought.
• In future iterations it would be better to refactor the code to stop repeatedly calculating the logits multiple times and then sampling from them. A single function that could handle that would be better.
• On that note, this implementation “works” but can be improved to be better. And that’s what’s in store for this project to stay tuned :)
• Full code here

Results

Future Work

Implementing PPO for continuous action in JAX. Benchmarking against MuJoCo tasks.

References

• CleanRL repository: https://github.com/vwxyzjn/cleanrl

• Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347. https://arxiv.org/abs/1707.06347